Pi-dämpare: Skillnad mellan sidversioner
Från Täpp-Anders
Hoppa till navigeringHoppa till sök
Anders (diskussion | bidrag) |
Anders (diskussion | bidrag) |
||
| Rad 14: | Rad 14: | ||
<math>R_2 = \frac{Z_2(K+1)-2\sqrt{KZ_1Z_2}}{K-1};</math> | <math>R_2 = \frac{Z_2(K+1)-2\sqrt{KZ_1Z_2}}{K-1};</math> | ||
<math>R_3 = \frac{2\sqrt{KZ_1Z_2}}{K-1};</math> | <math>R_3 = \frac{2\sqrt{KZ_1Z_2}}{K-1};</math> | ||
Om samma impedans önskas på båda sidor av PI-dämparen kan man förenkla till följande: | |||
<math>R_1 = R_2 = Z \left( \frac{\sqrt{K}-1}{\sqrt{K}+1} \right);</math> | |||
<math>R_3 = \frac{2Z\sqrt{K}}{K-1}</math> | |||
== T-dämparen == | == T-dämparen == | ||
Versionen från 16 februari 2013 kl. 04.34
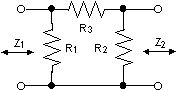
Pi-dämpare kännetecknas av att de är en delta-koppling med tre motstånd. Tricket här är att finna tre motstånd som låter kretsen behålla sin nominella impedans medan man låter dämpningen variera. Detta används bland annat för att justera dämpningen i radiokretsar eller för att anpassa mellan två olika impedanser, det senare görs genom att man gör pi-dämparen obalanserad.
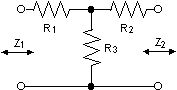
En variant är också T-dämparen som fungerar ungefär på samma sätt.
PI-dämparen
observera att effekten är en kvot, ej dB.
Om samma impedans önskas på båda sidor av PI-dämparen kan man förenkla till följande:
T-dämparen
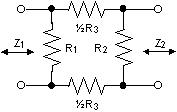
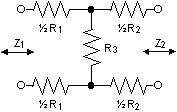
Betrakta följande varianter: