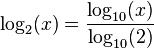Skillnad mellan versioner av "Shannon"
Anders (Diskussion | bidrag) (→2-logaritmen) |
(→Shannon på modemkanal) |
||
| (5 mellanliggande versioner av 2 användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| + | [[category:radio]] | ||
| + | [[category:Formelsamling]] | ||
| + | [[category:Informationsteori]] | ||
Shannons lag ger den maximala överförbara datatakten hos en given överföringskanal vid en viss effekt och ett givet signalbrusförhållande. | Shannons lag ger den maximala överförbara datatakten hos en given överföringskanal vid en viss effekt och ett givet signalbrusförhållande. | ||
| Rad 27: | Rad 30: | ||
Antag en bandbredd om 3600-300 Hz, dvs 3 500 Hz. Antag S/N 48 dB S/N så får vi följande: | Antag en bandbredd om 3600-300 Hz, dvs 3 500 Hz. Antag S/N 48 dB S/N så får vi följande: | ||
| − | <math>3\ 500 \cdot log_2(1+10^{48/10})</math> | + | <math>3\ 500 \cdot \log_2(1+10^{48/10})</math> |
| − | <math>\approx 3\ 500 \cdot log_2(1+63\ 095)</math> | + | <math>\approx 3\ 500 \cdot \log_2(1+63\ 095)</math> |
<math>\approx 3\ 500 \cdot 15,94</math> | <math>\approx 3\ 500 \cdot 15,94</math> | ||
<math>\approx 55\ 808</math> | <math>\approx 55\ 808</math> | ||
| Rad 34: | Rad 37: | ||
Man ser alltså att det krävs bra S/N för att klara 56 kbit/s modem... | Man ser alltså att det krävs bra S/N för att klara 56 kbit/s modem... | ||
| − | == 2-logaritmen == | + | == Omvandling till 2-logaritmen == |
Om din räknare inte kan hantera 2-logaritmen direkt så kan du omvandla från naturliga logaritmen <math>ln</math> eller tiotalslogaritmen <math>log_{10}</math> genom att använda följande omvanling: | Om din räknare inte kan hantera 2-logaritmen direkt så kan du omvandla från naturliga logaritmen <math>ln</math> eller tiotalslogaritmen <math>log_{10}</math> genom att använda följande omvanling: | ||
| Rad 40: | Rad 43: | ||
Naturliga logaritmen | Naturliga logaritmen | ||
| − | <math>log_2(x) = \frac{ln(x)}{ln(2)}</math> | + | <math>\log_2(x) = \frac{\ln(x)}{\ln(2)}</math> |
Tiotalslogaritmen | Tiotalslogaritmen | ||
| − | <math>log_2(x) = \frac{log_{10}(x)}{log_{10}(2)}</math> | + | <math>\log_2(x) = \frac{\log_{10}(x)}{\log_{10}(2)}</math> |
Nuvarande version från 9 augusti 2013 kl. 13.48
Shannons lag ger den maximala överförbara datatakten hos en given överföringskanal vid en viss effekt och ett givet signalbrusförhållande.
Grundformen
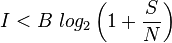
Där
- I är den informationshastighet i bitar per sekund
- B är den bandbredd överföringskanalen har i Hz
- S är den totala signalens effekt
- N är den totala bruseffekten i mottagaren
Vad lagen säger är alltså att den överförda mängden information i bit/s alltid måste vara mindre än bandbredden multiplicerad med den binära logaritmen av signalbrusförhållandet för överföringskanalen.
Shannon om GSM
Ett exempel på detta är en vanlig GSM-kanal med en mottagen signalstyrka på -90 dBm. Bruseffekten i en standard GSM-kanal kan räknas ut till -121 dBm så vi har ett S/N som är 31 dB. Detta ger oss då följande:
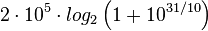
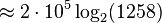
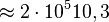
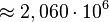
Så vi ser att normal GSM är ganska långt från shannons gräns. Vid -90 dBm räknar man med 270 kbit/s normalt och det innebär alltså 7,6 ggr från shannongränsen.
Shannon på modemkanal
Antag en bandbredd om 3600-300 Hz, dvs 3 500 Hz. Antag S/N 48 dB S/N så får vi följande:
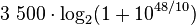
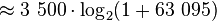
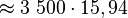
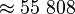
Man ser alltså att det krävs bra S/N för att klara 56 kbit/s modem...
Omvandling till 2-logaritmen
Om din räknare inte kan hantera 2-logaritmen direkt så kan du omvandla från naturliga logaritmen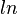 
eller tiotalslogaritmen 
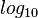genom att använda följande omvanling:
Naturliga logaritmen
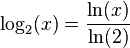
Tiotalslogaritmen
