Pi-dämpare

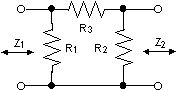
Pi-dämpare kännetecknas av att de är en delta-koppling med tre motstånd. Tricket här är att finna tre motstånd som låter kretsen behålla sin nominella impedans medan man låter dämpningen variera. Detta används bland annat för att justera dämpningen i radiokretsar eller för att anpassa mellan två olika impedanser, det senare görs genom att man gör pi-dämparen obalanserad.

En variant är också T-dämparen som fungerar ungefär på samma sätt vilken visas senare. Det går inte i en black box skilja en PI från en T-dämpare varför båda kan anses ekvivalenta i det ideala fallet.

Dessa beräkningar relaterar till Deltakoppling, Y-koppling av resistorer.

Dämpfaktorn

I alla nedanstående beräkningar är dämpfaktorn K uttryckt enligt

$K = \frac{P_1}{P_2}$

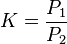
Dämpningen anges som en fraktion, ej i decibel och omräkningen från dB till fraktion ges naturligt av

$K=10^{A/10}$

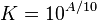
Där A är dämpningen i dB uttryckt som negativa dB. Exempelvis är 5 dB dämpning i ovanstående formel

$10^{-5/10} \approx 0,3162$

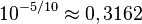
PI-dämparen

Ej balanserad PI-dämpare

Balanserad PI-dämpare

$R_1 = \frac{Z_1(K+1)-2\sqrt{KZ_1Z_2}}{K-1};$ $R_2 = \frac{Z_2(K+1)-2\sqrt{KZ_1Z_2}}{K-1};$ $R_3 = \frac{2\sqrt{KZ_1Z_2}}{K-1};$

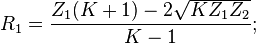
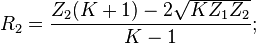
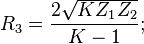
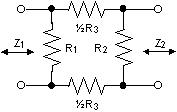
Om samma impedans önskas på båda sidor av PI-dämparen kan man förenkla till följande:

$R_1 = R_2 = Z \left( \frac{\sqrt{K}-1}{\sqrt{K}+1} \right);$ $R_3 = \frac{2Z\sqrt{K}}{K-1}$

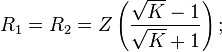
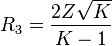
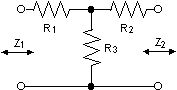
T-dämparen

Betrakta följande varianter:

Ej balanserad T-dämpare

Balanserad T-dämpare

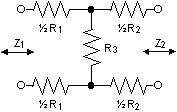
För en T-dämpare med olika impedanser på båda sidor enligt ovan kan följande sätt användas för att beräkna de lämpliga resistanserna:

$R_1=\frac{(K-1)Z_1\sqrt{Z_2}}{(K+1)\sqrt{Z_2}-2\sqrt{KZ_1}};$ $R_2=\frac{(K-1)Z_2\sqrt{Z_1}}{(K+1)\sqrt{Z_1}-2\sqrt{KZ_2}};$ $R_3=\frac{K-1}{2}\sqrt{\frac{Z_1Z_2}{K}};$

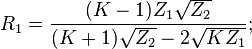
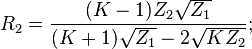
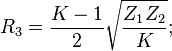
Vid samma impedans på båda sidor fås förenklingen:

$R_1=R_2=Z \left( \frac{\sqrt{K}+1}{\sqrt{K}-1} \right);$ $R_3=\frac{Z(K-1)}{2\sqrt{K}};$

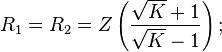
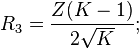
Hyperbolisk metod för Π- och T-dämparen

En variant på beräkningar som man sällan ser men kan dyka upp på de mest oväntade ställen är baserat på hyperboliska funktioner, vilket också gör att man kan använda komplexa värden i beräkningarna vilket är svårhanterat i den aritmetiska metoden ovan. I stället för att ange dämpningen i effektkvoten 'K' som i ovan aritmetisk lösningar så använder hyperboliska ekvationerna det logaritmiska måttet 'Neper' och betecknas Γ från önskad dB-värde enligt:

Observera! R1, R2 och R3 refererar till tidigare skisser precis som tidigare ekvationer gjort.

$\Gamma = \frac{dB} {8.686}\text{ Neper}$

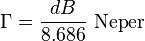
För 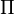$\Pi$-dämpare, symmetrisk med samma impedans på båda sidorna:

$R_3 = Z*\sinh(\Gamma)$

$R_1 = R_2 = \frac{Z}{\tanh(\frac{\Gamma}{2})}$

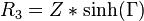
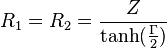
För osymmetrisk Π-dämpare, med olika impedans på respektive sida:

Först måste man räkna ut minsta möjlig dämpning för matchning mellan impedanserna Z1 och Z2 - gäller både T och Π-brygga:

$\Gamma = arcosh \Big(\sqrt{\frac {Z_1}{Z_2}}\Big)$

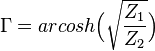
Värdet på Γ kan givetvis vara högre om man önskar mer dämpning.

Därefter motståndsvärdena för Π-dämparen:

$R_3 = \sqrt{(Z_1 * Z_2)} * \sinh(\Gamma)$

$\frac {1} {R_1} = \frac {1} {Z_1 * \tanh(\Gamma)} - \frac {1} {R_3}$

$\frac {1} {R_2} = \frac {1} {Z_2 * \tanh(\Gamma)} - \frac {1} {R_3}$

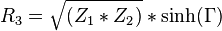
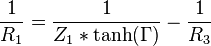
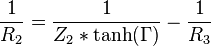
För T-dämpare, symmetrisk med samma impedans på båda sidorna:

$R_3 = \frac {Z} {\sinh(\Gamma)}$

$R_1 = R_2 = Z * \tanh(\frac{\Gamma}{2})$

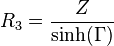
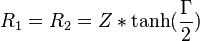
För osymmetrisk T-dämpare med olika impedans på respektive sida:

$R_3 = \sqrt{(Z_1 * Z_2)} * \sinh(\Gamma)$

$R_1 = \frac {Z_1}{\tanh(\Gamma)} - R_3$

$R_2 = \frac {Z_2}{\tanh(\Gamma)} - R_3$

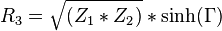
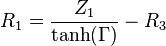
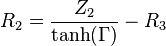
Exempel

$\Gamma = \frac{4 dB} {8.686} = 0.4605 \text{ Neper;}$

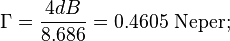
Därefter för Π-brygga för samma impedanser på var sida

$Z = Z_1 = Z_2 = 50 \Omega$

$R_3 = Z*\sinh(\Gamma)=50*\sinh(0.4605) = 23.87 \Omega$

$R_1 = R_2 = \frac{Z}{\tanh(\frac{\Gamma}{2})} = \frac{50} {\tanh(\frac{0.4605}{2})}=220.98 \Omega$

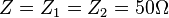
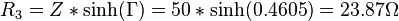
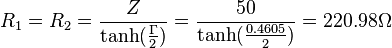
Det är allt - enkelt eller hur, ingen rottecken eller någonting i och med att man tog steget att gå över till Neper i stället för dB så använder man den naturliga logaritmen (ln) i stället för tiotalslogaritmen (log₁₀) och det innebär förenklingar i matematiken.

Med Π-brygga kan man också anpassa mellan olika impedanser, och enligt följande hyperboliska metoder:

Kontrollera först hur mycket minimumloss för att gå mellan 50 Ohm (Z1) till 25 Ohm (Z2) matchning - under dess dämpning så blir resultatet motstånd med negativ resistans - vilket också indikerar att man har räknat fel, om man nu inte använder NIC (negative impedance converter) i sin lösning:

$cosh(\Gamma) = \sqrt{\frac{Z_1} {Z_2}}$

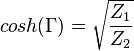
Omstuvat och för 50 Ohm till 25 Ohm:

$\Gamma = arcosh \Big(\sqrt{\frac {50 \Omega}{25 \Omega}}\Big) = arcosh(1.4147) = 0.8814$

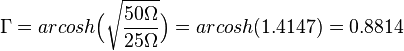
Och för att göra om till dB:

$\text{dB} = \Gamma * 8.686 = 0.8814 * 8.686 = 7.66 \text{ dB}$

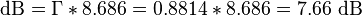
7.66 dB är alltså minimum dämpning vid resistiv matchning mellan 50 Ohm och 25 Ohm system

Räkna ut aktuella motstånd:

$R_3 = \sqrt{(Z_1 * Z_2)} * \sinh(\Gamma) = \sqrt{ 50 * 25} * \sinh(0.8814) = 35.355 \Omega$

$R_3 = 35.355 \Omega$

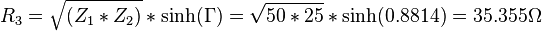
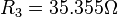
i seriemotstånd mellan 50 > 25 Ohm system.

$\frac {1} {R_1} = \frac {1} {Z_1 * \tanh(\Gamma)} - \frac {1} {R_3} = \frac {1} {50 * \tanh(0.8814)} - \frac {1} {35.355} = \frac {1} {inf.}$

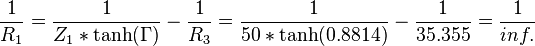
R1 = oändligt hög - motstånd på 50 Ohm sidan behövs ej här

$\frac {1} {R_2} = \frac {1} {Z_2 * \tanh(\Gamma)} - \frac {1} {R_3} = \frac {1}{25 * \tanh(0.8814)} - \frac {1} {35.355} = \frac {1} {35.355 }$

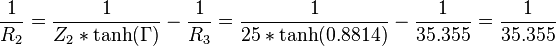
35.355 Ohm mot jord på 25 Ohm sidan

Vill man ha mer dämpning utöver minimumvärdet i anpassningen så använder man sig av:

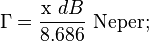$\Gamma = \frac{\text{x }dB} {8.686} \text{ Neper;}$ för önskad 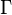$\Gamma$ i ovanstående uträkning.